Numération binaire.
Les informations que doivent traiter les ordinateurs sont composées de chiffres, de lettres ou de symboles particuliers. La première forme de représentation a été celle des nombres.
Afin d’être assimilable par la machine les informations doivent être codées sous forme binaire.
En langage binaire l’information est représentée sous forme de 0 et de1.
I. Conversion d'un nombre décimal dans une base de numération b
Pour permettre de stocker les bits dans la mémoire, il convient de les coder préalablement. Pour cela il existe deux méthodes.
La première consiste à effectuer des divisions successives par b jusqu'à obtenir un quotient inférieur à b. Le dernier quotient de la dernière division et les différents restes des divisions donnent l'écriture du nombre décimal en base de numération b.
La deuxième méthode consiste à effectuer des soustractions successives de puissances de b maximales jusqu'à obtenir 0.
Exemples.
1) N = 67 et b = 2
Première méthode 67 2 1 33 2 1 16 2 0 8 2 0 4 2 0 2 2 0 1 N = (67)10 = (1000011)2 |
Deuxième méthode 67 64 1 * 26 3 2 1 * 21 1 1 1 * 20 0 N = (67)10 = (1000011)2 |
2) N = 67 et b = 5
Première méthode 67 5 2 13 5 3 2 N = (67)10 = (232)5 |
Deuxième méthode 67 50 2 * 52 17 15 3 * 51 2 2 2 * 50 0 N = (67)10 = (232)5 |
II. Conversion d'un nombre de base b en base décimale
Soit an, an-1, ..., a2, a1, a0 un nombre de n chiffre écrit en base b. On peut le représenter de la façon suivante :
bn |
bn-1 |
... |
b2 |
b2 |
b1 |
an |
an-1 |
... |
a2 |
a1 |
a0 |
Pour convertir ce nombre en base décimale, il suffit de poser l'opération suivante :
N (en base 10) = an x bn + an-1 x bn-1 + ... + a2 x b2 + a1 x b1 + a0 x b0
Exemples.
1) N = 341 et b = 5
52 |
51 |
50 |
3 |
4 |
1 |
ainsi N (en base 10) = 1 x 50 + 4 x 51 + 3 x 52 = 1 + 20 + 75 = (96)10
2) N = 101110 et b = 2
25 |
24 |
23 |
22 |
21 |
20 |
1 |
0 |
1 |
1 |
1 |
0 |
ainsi N (en base 10) = 0 x 20 + 1 x 21 + 1 x 22 + 1 x 23 + 0 x 24 + 1 x 25 = 0+2+4+8+0+32=46
III. Les opérations arithmétiques dans le système binaire
A. Conversion.
Base 10→base 2 : divisions successives par 2…
Base 2→base 10 : puissances…
Un élément binaire = 1 bit ( ≠ 1 byte = 1 octet = 8 bits ).
Stockage sous forme de mots mémoires qui comprennent soit 4 bits, soit 8 bits…128 bits.
128 symboles→7 positions binaires + une pour le contrôle de parité.
B. L'addition
On note r la retenue et u l'unité du résultat de l'addition de deux chiffres binaires. La table d'addition élémentaire est la suivante :
+ |
0 |
1 |
||
0 |
r = 0 |
u = 0 |
r = 0 |
u = 1 |
1 |
r = 0 |
u = 1 |
r = 1 |
u = 1 |
Réalisation de l'addition 11011101 + 11101110
1 1 1 1 1 1 0 0 ç retenues
1 1 0 1 1 1 0 1
+ 1 1 1 0 1 1 1 0
![]()
1 1 1 0 0 1 0 1 1
C. La soustraction
La table de soustraction est la suivante :
- |
0 |
1 |
||
0 |
r = 0 |
u = 0 |
r = 0 |
u = 1 |
1 |
r = 1 |
u = 1 |
r = 0 |
u = 0 |
Réalisation de la soustraction 1110101 - 1111
1 1 1 0 1 0 1
1 1 1
- 1 1 1 1
1 1 1
![]() 1 1 0 0 1 1 0
1 1 0 0 1 1 0
D. La multiplication
Les multiplications binaires s’effectuent selon le principe de la multiplication décimale. On multiplie doc le multiplicande par chacun des bits du multiplicateur, on décale les résultats intermédiaires obtenus et on effectue ensuite l’addition de ces résultats partiels.
Réalisation de la multiplication

E. La division
Inversement, la division va être basée sur une succession de soustractions et s’emploie de la même façon qu’une division décimale ordinaire.
Réalisation d’une division

Cas des nombres fractionnaires
Les nombres utilisés jusqu’à présent étaient des entiers positifs ou négatifs. Bien sûr il est également possible de rencontrer des nombres fractionnaires. Dans ce cas la partie décimale se traduit en mettant en œuvre des puissances négatives de 2 et en pratiquant comme pour la partie entière d’un nombre.
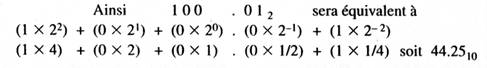


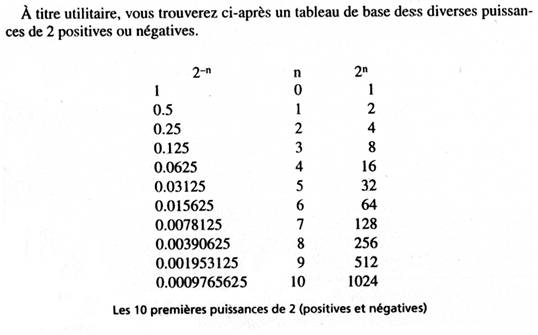
IV. La représentation des nombres
Les systèmes informatiques manipulent des informations binaires et travaillent en général sur une longueur fixe de bits que l’on appelle mot.
Suivant la machine, la taille du mot sera différente, les tailles classiques étant : 16, 32, 64 bits.
On rencontre aussi des notions de double-mot ou demi-mot.
0000 |
|||||||
Quartet |
|||||||
Octet |
Ou ici demi-mot |
||||||
Mot de 16 bits |
|||||||
Double-mot |
|||||||
A. La numération décimale codée binaire (DCB).
Les nombres stockés sous forme DCB occupent pour chaque chiffre décimal un quartet : + rapide et + facile à convertir car on fait une représentation binaire de chaque chiffre et non de l’ensemble. (ex : 148→0001|0100|1000 )
B. La numération hexadécimale.
Repose sur un alphabet de seize symboles ( 0→9 , A→F )
- Conversion de base 10 en base 16 : divisions successives.
- Conversion de base 16 en base 10 : multiplication s successives des puissances de seize.
→ Passage du binaire à l’hexadécimal.
Pour chaque symbole de l’alphabet hexadécimal : utilise au maximum 4 bits.
- Conversion de base 2 en base 16 : décomposition en blocs de 4 bits en partant de la droite.
- Conversion de base 16 en base 2 : convertir chaque chiffre hexa en binaire.
Avec un demi-mot mémoire d’1 octet et 1 bit de signe : compte de +127 à -128 ( 0 est chiffre+ ). 00 à FF.
Avec un mot-mémoire de 16 bits : compte de +32767 à -32768. ( 0000 à FFFF )
Avec un mot-mémoire de 4 octets : compte de +2147483647 à -2147483648. ( 00000000 à FFFFFFFF ).
C. Le code ASCII. (voir table fournie en annexe)
Code ASCII 7 bits → 128 combinaisons. 8e bit : bit de contrôle.
Ce 8eme bit parfois pas utilisé → 8 bits pour 256 combinaisons, ASCII étendu.
D. EBCDIC : Extended Binary Coded Decimal Interchange Code.
Equivalent à l’image miroir du l’ASCII.
Code destiné à la communication et crée par IBM.
E. Le code UNICODE ( code à 16 bits ).
Code destiné à devenir code universel, permettant de coder le cyrillique ou les idéogrammes japonais.
V. La représentation des nombres négatifs
A. Première méthode
Elle consiste à représenter un nombre par :
* son signe avec la convention suivante : 0 pour un nombre positif, 1 pour un nombre négatif
* sa valeur absolue convertie en binaire pur.
Exemple : représentation de (+11) et (-38)
* représentation de (+11)
00001011 avec le premier 0 pour le signe et les 7 bits suivants pour le codage de 11
* représentation de (-38)
|38| = 0100110
donc (-38) = 10100110
B. Deuxième méthode : le complément à deux
Elle consiste à représenter un nombre signé par :
* sa représentation en signe et valeur absolue pour un nombre positif
* la représentation en complément à deux de |N| lorsque celui ci est négatif (on inverse tous les bits et on ajoute 1). La convention de signe est toujours respectée.
Exemple : représentation de (+27) et (-9)
* représentation de (+27)
(27) = 11011
* représentation de (-9)
(9) = 00001001
00001001 en complément à 1 -> 11110110
en complément à 2 -> 11110110 + 1 = 11110111 = (-9)